- © 2008 Canadian Medical Association
Recently, several articles have been published that advocate an alternative method for calculating the number needed to treat to assess the effects of medications in clinical trials.1,2 This new method, which gives an “event-based” number needed to treat, calculates the number needed to treat based on outcomes that can occur more than once in the same patient, instead of dichotomous outcomes that only occur once in each patient during a given period.
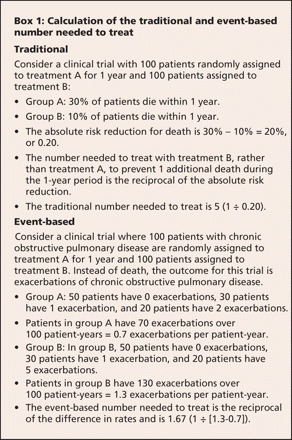
The number needed to treat is traditionally defined as the reciprocal of the absolute risk reduction.3,4 It was originally meant to be calculated for dichotomous events (e.g., death, myocardial infarction) that occurred once in each patient during a particular period.5 The number needed to treat can also be applied to continuous or ordinal outcomes if the outcome can be dichotomized into 2 discrete categories (e.g., the proportion of patients who attain the expected minimal clinically important difference in the outcome).6,7 The number needed to treat represents the estimated number of patients who need to receive a treatment, compared to a control, for 1 additional patient to benefit. An example of how to calculate a traditional number needed to treat is shown in Box 1.
An alternative approach: the “event-based” number needed to treat
Recent studies have described an alternative method for calculating the number needed to treat.1 Studies that use this method define the event-based number needed to treat as “the reciprocal of the difference between the treatment and control groups in the rate of a particular outcome per patient within a given time frame.”1 Using this definition, the rate of events per patient-year is calculated for the treatment and control groups. The reciprocal of the difference in rates is used to calculate an event-based number needed to treat.1,2
Since being introduced into the medical literature in 2005,1 the event-based number needed to treat has been used extensively to describe results of respiratory clinical trials. In a recent clinical trial, Kardos and colleagues found that the rate of exacerbations of chronic obstructive pulmonary disease was 0.92 per patient per year among patients randomly assigned to treatment with fluticasone and salmeterol, and 1.4 per patient per year among those randomly assigned to receive salmeterol.8 The authors calculated the number needed to treat to be 2.08 (1 ÷ [1.4–0.92]). They therefore stated that the number of patients needed to treat with fluticasone and salmeterol rather than salmeterol alone to prevent 1 exacerbation of chronic obstructive pulmonary disease per year was 2.08. Similarly, the recently published Towards a Revolution in COPD Health (TORCH) trial observed an annual rate of exacerbations of 0.85 in the fluticasone and salmeterol group and 1.13 in the placebo group. The authors calculated a number needed to treat of 4 (1 ÷ [1.13–0.85]), implying that 4 additional patients need to receive fluticasone and salmeterol to prevent 1 exacerbation over 1 year.9 The event-based number needed to treat has also been used to describe the effects of nonpharmacologic interventions for chronic obstructive pulmonary disease, such as nurse-led intermediate care programs for prevention of unscheduled physician visits.10
False exaggerations of treatment benefits
Unfortunately, the above method for calculating the number needed to treat may be misleading because the number needed to treat as used in this context has no theoretical foundation. This number cannot be correctly applied to recurring events in the same patient (such as exacerbations of chronic obstructive pulmonary disease) because a summation of these individual events does not follow a binary distribution.
In fact, in clinical trials, as in real life, a large proportion of patients will have no exacerbations of chronic obstructive pulmonary disease in 1 year, some patients will have 1 or 2 exacerbations and a few patients will experience multiple exacerbations.
Consider the example outlined in Table 1 where 10 patients are randomly assigned to placebo for 1 year and 10 patients are assigned to treatment for 1 year. The treatment is designed to prevent exacerbations of chronic obstructive pulmonary disease. In this example, 1 patient in the placebo group experiences a single exacerbation in 1 year, 2 patients experience 6 exacerbations and the remaining patients have none. In total, patients in the placebo group experienced 13 exacerbations over 10 patient-years, or 1.3 exacerbations per patient-year. In contrast, in the treatment group, 1 patient has 3 exacerbations and 1 patient has 5. The remaining patients have none. In total, patients in the treatment group experience 8 exacerbations over 10 patient-years, or 0.8 exacerbations per patient-year. Calculation of the traditional measure of number needed to treat yields a number needed to treat of 10 (1 ÷ [0.3–0.2]). However, the event-based number needed to treat is 2 (1 ÷ [1.3–0.8]).
Table 1.
The clinical implication of this event-based number needed to treat is that on average, if 2 additional patients received the treatment, 1 exacerbation will be prevented. Or expressed another way, the event-based number needed to treat implies that each patient who receives treatment has a 1 in 2 chance of benefiting from treatment. However, from the data it is apparent that if a clinician treats the next 2 patients with chronic obstructive pulmonary disease who enter into his or her office, in all probability, exacerbations would not be prevented at all, because in this example, the treatment exerts no measurable effect in 70% of patients who receive treatment. The event-based number needed to treat yields a result that is 5-fold smaller than the traditional number needed to treat. This is because the event-based number needed to treat is heavily influenced by a minority of patients who may experience multiple exacerbations. This statistic, therefore, can provide misleading information because it does not correctly describe the effect of extending treatment out to the population at large.
Consider an alternative situation where 10 patients are randomly assigned to receive placebo for 1 year and 10 patients are assigned to receive treatment to prevent exacerbations of chronic obstructive pulmonary disease. In this example, 1 patient in the placebo group experiences a single exacerbation during the 1 year period, 2 patients experience 8 exacerbations and the remaining patients have none. In total, patients in the placebo group have experienced 17 exacerbations over 10 patient-years, or 1.7 exacerbations per patient-year. In contrast, 2 patients in the treatment group each experience 2 exacerbations and the rest have none. In total, patients in the treatment group experience 4 exacerbations over 10 patient-years, or 0.4 exacerbations per patient-year. The event-based number needed to treat in this example is 0.77 (1 ÷ [1.7–0.4]). This suggests that 0.77 patients would have to receive treatment to prevent a single exacerbation. Clearly it is impossible for 0.77 of a patient to receive treatment. Thus, this statistic has no legitimate clinical interpretation. If the number needed to treat of 0.77 is rounded to 1, it implies that treatment is indicated for every patient because treatment would prevent exacerbations for all patients. Review of the actual data indicates that clearly this is not the case, because 70% of patients in this example would not experience any benefit of treatment. Again, the event-based number needed to treat provides misleading information.
Instead, the number needed to treat should be calculated based on the difference in the proportion of patients who experience 1 or more exacerbations during the trial period. An example of the correct use of the number needed to treat statistic to describe exacerbations of chronic obstructive pulmonary disease can be taken directly from previous clinical trials. As described in the trial by Kardos and colleagues, 241 of 487 (49.5%) patients who received salmeterol and 210 of 507 (41.4%) patients who received salmeterol and fluticasone had at least 1 exacerbation during the 44 week trial.8 Therefore, the absolute risk reduction was 8.1% (49.5%–41.4%). The number needed to treat for salmeterol and fluticasone (rather than salmeterol alone) to prevent 1 additional patient from experiencing an exacerbation in 44 weeks was 12.3 (1 ÷ 0.081). The traditional number needed to treat of 12.3 is much greater than the event-based number needed to treat of 2.0 reported by the Kardos and colleagues.11
Conclusion
The number needed to treat can be applied with confidence to binary outcomes such as mortality rates. It can also be applied to continuous or ordinal outcomes that can be dichotomized. However, the number needed to treat should be interpreted with caution if it is applied to recurrent events that occur in the same patients over time. In this situation, the number needed to treat may be misleading, especially if some patients have many recurrent events and other patients have no events. If applied to recurrent event data, the event-based number needed to treat may lead clinicians to overprescribe therapies based on statistically incorrect and artificially inflated numbers needed to treat.
Application of the event-based number needed to treat has been limited thus far to clinical trials of interventions designed to prevent exacerbations of chronic obstructive pulmonary disease. However, patients with other chronic conditions, such as asthma, multiple sclerosis or sickle cell anemia, also experience recurrent exacerbation events over time. It is likely that the event-based number needed to treat will eventually be applied to these conditions as well. Thus, clinicians need to be aware of the potential for exaggeration of treatment benefits if this statistic is improperly applied.
-
The number-needed-to-treat statistic has been used for years in clinical medicine.
-
It is traditionally calculated as the reciprocal of the absolute risk reduction.
-
The “event-based” number needed to treat is meant to be applied to recurrent events, such as exacerbations of chronic obstructive pulmonary disease.
-
The event-based number needed to treat may be misleading because it is heavily influenced by a minority of patients who experience multiple recurrent events.
-
Use of the number needed to treat for recurrent events may provide results that falsely exaggerate the beneficial effects of treatments in clinical trials.
Key points
Footnotes
-
For a further discussion about the use and misuse of the number needed to treat, see the Analysis article by Finlay McAlister in the September 9 issue (CMAJ 2008;179:549-53).
This article has been peer reviewed.
Contributors: Shawn Aaron wrote the first draft of the manuscript. Both of the authors critically revised the manuscript for important intellectual content and approved the final version submitted for publication.
Competing interests: None declared.
REFERENCES
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.