Clinical prediction models aim to predict individual clinical outcomes using multiple predictor variables. Prediction models are abundant in the medical literature and their number is increasing.1–3 Established causal risk factors are often good predictors. For example, the Framingham Risk Score, which predicts the 10-year risk of cardiovascular disease, includes the variables blood pressure and smoking status, which are well-established risk factors.4 However, predictors are not necessarily causally related to the clinical outcome, for example, tumour markers in cancer progression or recurrence.
Even though causality is not certain, clinical researchers often anticipate a particular direction in the relation between predictor and outcome. For example, higher blood pressure is expected to increase and not decrease the risk of cardiovascular disease.4 Thus, a negative association between blood pressure and cardiovascular disease (suggesting a protective effect) is unexpected and unlikely to be found in another population. It could, consequently, hamper generalizability. Moreover, unexpected findings may suggest that the prediction model is invalid, thus lowering the face validity of the model, such that readers and potential users will not trust the model to guide their practice.5
Our aim is to describe causes for unexpected findings in prediction research and to provide possible solutions. In the first section, we describe 3 clinical examples that will be used for illustrative purposes throughout the paper. The subsequent section outlines causes for unexpected findings and their potential solutions, followed by a general discussion.
Clinical examples
We use data from 3 prognostic studies in which an unexpected predictor–outcome relation was found during the development of the prognostic model. Using these studies, we illustrate causes and solutions for unexpected findings in clinical prediction research. For illustration purposes, we use selective samples of the original data; the validity of the original models is not questioned in any way.
Example 1. Metabolic acidosis in neonates
Metabolic acidosis in neonates is associated with several short- and long-term complications, including death. Westerhuis and colleagues6 developed a prediction model to identify as early as possible women at risk of giving birth to a child with metabolic acidosis, which can be the result of a lack of oxygen in the fetus. Because an elevated maternal body temperature leads to more oxygen consumption, it was unexpected that a higher maternal body temperature actually reduced the risk of neonatal metabolic acidosis.6
Example 2. Diagnosing deep vein thrombosis
Deep vein thrombosis is a serious condition with potentially lethal complications, such as pulmonary embolism. The common practice is to diagnose deep vein thrombosis with ultrasonography, which requires referral to a radiology department. Oudega and colleagues7 developed a prediction model to diagnose deep vein thrombosis. In general, deep vein thrombosis is less common among men than women.8,9 Therefore, the observation that male sex increased the probability of a diagnosis of deep vein thrombosis was unexpected.7
Example 3. Anemia in whole-blood donors
To prevent iron deficiency in donors after blood donation and to guarantee high quality of donor blood, the iron status of blood donors is assessed before donation by measuring hemoglobin levels. Deferrals are demoralizing for donors and increase the risk of subsequent donor lapse. Baart and colleagues10 developed 2 sex-specific models to predict low hemoglobin levels in whole-blood donors. The total number of whole-blood donations in the past 2 years was expected to increase the chance of low hemoglobin levels but, unexpectedly, lowered the probability of low hemoglobin levels.
Causes and solutions
Causes for unexpected findings in prediction research include chance, misclassification of the predictor, selection bias, mixing of effects (confounding), intervention effects and heterogeneity (Table 1). One rigorous solution that appeals to all causes for unexpected findings is to delete the predictor with the unexpected finding from the model. However, this is undesirable as it likely reduces the predictive ability of the clinical prediction model11 and reduces face validity of the model. Hereafter, we will discuss the causes and solutions depicted in Table 1 and illustrate these using the aforementioned clinical examples.
Causes of and solutions for unexpected findings in prediction research
Chance
The direction of the found (estimated) predictor–outcome relation may be opposite from the anticipated direction merely by chance. For example, the observed relation between gestational age and neonatal metabolic acidosis (example 1) was observed to be an odds ratio (OR) of 1.17 (95% confidence interval [CI] 1.09–1.27), which is in line with clinical experience (i.e., expected) because the chance of metabolic acidosis increases with increasing gestational age. However, if we take random samples from this dataset, by chance we may observe an opposite relation. For example, we took 1000 random samples of size 50, 100, 250, 500 or 1000 participants from this same data source. Among these samples, the proportion of unexpected findings (OR < 1) decreased with increasing sample size: 37.3%, 33.5%, 25.4%, 18.3% and 11.0%, respectively. Hence, the probability of observing an unexpected finding of the predictor–outcome relation by chance strongly depends on sample size.
Misclassification
The status of a predictor may be measured or coded with error (e.g., coding women with intrapartum fever as women without and vice versa) and hence may lead to incorrect classification (i.e., predictor misclassification). Furthermore, the predictor–outcome relation may be modelled incorrectly, for example, when an incorrect transformation is used for a continuous predictor (e.g., linear instead of nonlinear) or when a continuous variable is categorized.3,12 Finally, collinearity of variables may result in apparent misspecification. Collinearity arises when 2 or more predictors are highly correlated and so explain similar components of the variability in patient outcome. For example, body mass index and weight are by definition strongly correlated. Including these predictors together can lead to poor estimation of the individual predictor estimates, in particular an inflated standard error and low power, which may increase the possibility of unexpected findings. However, in terms of predictive accuracy of the overall model, collinearity will usually not affect performance as long as the collinearities in future data are similar to those identified in the data used to develop the model.
Possible solutions for misclassification of a predictor include redoing the measurement (if possible) and modelling the continuous predictor appropriately (e.g., by splines or fractional polynomials).13 Alternatively, if it is known which values are measured with significant error, these could be deleted and imputed.14 In the case of collinearity, options include omitting some of the affected predictor variables from the model, or combining them into a single variable (e.g., mean arterial pressure instead of systolic and diastolic blood pressure) by adding or summing them. However, it may be entirely sensible to include collinear predictors together in the model to improve the overall predictive accuracy. In this situation, an important recommendation is to interpret any collinear predictors in combination, rather than separately. For example, in a model in which the highly collinear variables age and age squared are both included, one should discuss the quadratic relation due to age and not focus on the individual estimates for age or age squared. A more extreme solution is to adopt a different regression technique, such as ridge regression, but this itself may lead to biased predictor effect estimates and make the model hard to interpret.
Misclassification was a potential cause of the unexpected finding in the example of predicting risk of metabolic acidosis in neonates (example 1). After reclassification of intrapartum fever from 37.8°C to 38.5°C, the initial unexpected finding in the predictor outcome relation (OR 0.86 [95% CI 0.68–1.08]) disappeared (OR 1.43 [95% CI 0.99–2.08]).6 The choice of temperature (threshold value) to define fever is thus influential in the direction of the predictor effect, and a better approach may be to analyze temperature as a continuous predictor.
Selection bias
If the study population is a selective sample from the total patient population (domain), this may result in biased estimates, for example, when the selection is related to both the predictor and the outcome. Selection bias can occur at different phases during a study, for example, at inclusion (e.g., index event bias), during follow-up (e.g., selective dropout) or during the measurement of the outcome at interest (e.g., when not all patients undergo the same reference test, referred to as differential verification).15
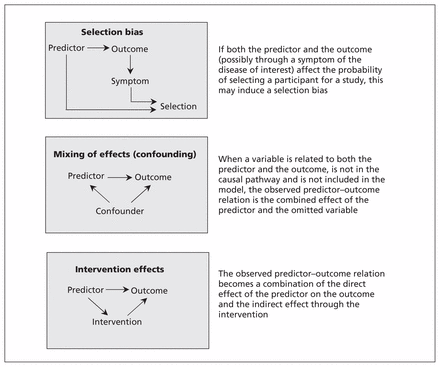
The mechanism resulting in selection bias is schematically shown in Figure 1. If both the predictor and the outcome (possibly through a symptom of the disease of interest) affect the probability of selecting a participant for a study, this may induce a bias (i.e., selection bias). A possible solution for selection bias is to apply weighting, in which a subgroup can be given extra weight to compensate for possible under-representation.16 The extent of the underrepresentation, however, is typically unknown, and the weights will therefore depend on unverifiable assumptions.16 Another solution is to clearly define the domain in which the model is applicable (e.g., only among patients with suspected deep vein thrombosis in secondary care).
Directed acyclic graphs of scenarios that may result in unexpected findings in prediction research.
In the diagnostic study on deep vein thrombosis (example 2), men unexpectedly had a higher probability of a diagnosis of deep vein thrombosis than women (OR 1.84 [95% CI 1.41–2.40]). This may be owing to an overrepresentation of women without deep vein thrombosis in the study population. If female sex is a risk factor for deep vein thrombosis, primary care physicians may suspect deep vein thrombosis more often in women than in men, and consequently more women without deep vein thrombosis might be referred to secondary care. If we assume that women were twice as likely to be included in the study compared with men, the unexpected finding disappears by weighting these overrepresented women without deep vein thrombosis with 1/2 (i.e., 1 divided by the likelihood of inclusion in the study) in the multivariable regression model (OR 0.92 [95% CI 0.62–1.36]).
The problem of selection bias can be extended to meta-analyses, which may have publication and selective-reporting biases. An example is the meta-analysis of Tandon and colleagues,17 which found that the presence of mutant p53 tumour suppressor gene is prognostic for disease-free survival (hazard ratio [HR] 0.45 [95% CI 0.27–0.74]) but not for overall survival (HR 1.09 [95% CI 0.60–2.81]) in patients presenting with squamous cell carcinoma arising from the oropharynx cavity. Of the total 6 studies included in the meta-analysis, all reported on the prognostic effect of p53 for overall survival, but only 3 for disease-free survival. Results on disease-free survival were reported only when deemed prognostic; thus, there appears to be a selective availability of data, leading to unexpected findings.18 A possible solution to this problem is to perform a bivariate meta-analysis, which synthesizes both outcomes jointly and accounts for their correlation,19 to reduce the impact of missing disease-free survival results in 3 studies by “borrowing strength” from the available overall survival results. A bivariate meta-analysis gave similar overall survival conclusions but gave an updated summary HR for disease-free survival of 0.76 (95% CI 0.40–1.42), indicating no significant evidence that p53 is prognostic for disease-free survival.18
Mixing of effects (confounding)
When 2 causes of a disease are mutually related, the observed effect of one can be mixed up with the effect of the other. In causal research, this phenomenon is referred to as confounding. Similarly, if 2 factors are mutually related (e.g., smoking and alcohol consumption) and one is causal for the outcome but the other is not, then exclusion of the causal factor would lead to the noncausal factor having a strong predictor effect unexpectedly. For example, omitting smoking from a prediction model for lung cancer would lead to alcohol consumption unexpectedly predicting lung cancer risk simply because it is confounded by smoking (those who smoke more tend to drink more). Because in prognostic research, the interest lies in the joint predictive accuracy of multiple predictors, confounding is usually not deemed relevant.20 However, the mechanism is the same in both descriptive and causal research: when omitting from the model a variable that is related to both an included predictor and the outcome, the observed predictor–outcome relation is the combined effect of the included predictor and the omitted variable (Figure 1). Consequently, an unexpected finding of the predictor–outcome relation can be observed. The potential for mixing of effects is specific to the design and population. Hence, mixing of effects likely affects generalization of the model to other populations. An obvious solution would be to include the variable that was initially omitted from the prediction model; however, this is impossible when the variable is not observed.
Mixing of effects was observed in the example of predicting anemia in whole-blood donors (example 3). A lower risk of low hemoglobin levels was found when the number of whole-blood donations in the past 2 years increased (OR 0.92 [95% CI 0.90–0.93]), also known as the “healthy donor effect,” which was corrected by including the recent history of hemoglobin level to the model (OR 1.00 [95% CI 0.98–1.02]). The most recent historic value of hemoglobin level is related to both the current hemoglobin level and the current risk of anemia, and is thus a confounder.
Intervention effect
Predictor values may guide the decision to start a medical intervention. If effective, this intervention then lowers the probability of the outcome, thus attenuating the observed predictor–outcome relation. Similar to the mixing of effects, the overall observed relation is a combination of the direct effect of the predictor on the outcome and the indirect effect through the intervention (Figure 1). However, expectations of the direction of the predictor–outcome relation apply to the direct effect. Theoretically, the overall observed predictor–outcome relation could even be the reverse of the direct effect between predictor and outcome (in the case of an extremely effective intervention), thereby leading to an unexpected finding. Without further consideration, it seems unlikely that an intervention reduces the risk of the outcome to a level that is even lower than observed in a group who didn’t have the indication and therefore didn’t receive the intervention.
The solution to deal with an unexpected finding due to an intervention effect would be to include the intervention in the prediction model.21 Clearly, this is not possible if everyone in the study has the same intervention. In that case, it is likely that the unexpected finding actually has another cause than an intervention effect. If an intervention is equally effective in all patients, modelling the intervention effect doesn’t require an interaction between predictor and intervention in the model. If the intervention is more effective in, for example, those having the predictor, then an interaction between intervention and predictor is required (see Heterogeneity).
In the prediction of metabolic acidosis in neonates (example 1) there could be an intervention effect present owing to cesarean delivery. An unexpected finding was observed for the relation between intrapartum fever and metabolic acidosis (OR 0.86 [95% CI 0.68–1.08]). Upon inclusion of cesarean delivery in the model, intrapartum fever was positively related to metabolic acidosis (OR 1.08 [95% CI 0.86–1.34]), which was in line with expectations.
Heterogeneity
The effect of a predictor may differ across subgroups of patients. This is referred to as a differential predictor effect, interaction, effect modification or heterogeneity of the predictor. When heterogeneity is not accounted for in the prediction model, the observed predictor effect is a (weighted) average of predictor effects within the different subgroups. If the predictor–outcome relations across subgroups are opposite, the direction of the observed relation depends on the proportional contributions of the subgroups. Expectations are likely based on the majority subgroup in a typical patient population, which is not necessarily the majority in the study population. Hence, heterogeneity of a predictor effect can lead to unexpected findings if not accounted for. This differs from selection bias, in that the relative size of the subgroups is not related to both predictor and outcome. The principal solution to deal with heterogeneity is to include an interaction term in the model.
Heterogeneity is an unlikely cause for an unexpected finding in prediction models. First, heterogeneity that results in genuinely opposite direction of effects is rare in epidemiology. Second, it seems unrealistic to assume that the group of patients who are typically the majority represent only the minority of patients in a specific study population.
In the prognostic model of metabolic acidosis in neonates (example 1), the effect of intrapartum fever on metabolic acidosis (OR 0.86 [95% CI 0.68–1.08]) was unexpected. Alongside the impact of misclassifying the presence of fever (see Misclassification), this unexpected finding could also have been the result of an interaction between intrapartum fever and epidural analgesia among women who received epidural analgesia (OR 0.47 [95% CI 0.35–0.64]) versus women without epidural analgesia (OR 3.16 [95% CI 2.16–4.64]).
Discussion
A first step in evaluating the validity of a clinical prediction model is to check whether the direction of the predictor–outcome relation is as expected. We identified 6 causes for unexpected findings: chance, misclassification, selection, mixing of effects (confounding), intervention effects and heterogeneity. The aforementioned causes for unexpected findings can occur simultaneously. In that instance, finding the reasons for the unexpected finding will become more complicated, yet the solutions described still hold and can be applied simultaneously.
The major problem of an unexpected finding in prediction research is that it may hamper the generalizability of a prediction model. Even though the performance of the model may be good in the population in which the model was developed, it will probably be weaker when applied to a different setting or population, indicating poor generalizability. Hence, despite high methodologic standards used in the development of the model it will not (i.e., not without further adjustments3,22) be applicable outside the population in which it was developed. It is therefore of utmost importance to signal unexpected findings. When the direction of a predictor–outcome relation is well-established in both the literature and in clinical experience, it is easy to identify unexpected (or incorrect) findings. Things become complicated when there is no pre-existing knowledge and it is unknown what direction is to be expected. Then, one has to make assumptions on the relation, and therefore it is called an unexpected finding rather than an incorrect finding. A more subtle unexpected finding occurs when the direction of a predictor–outcome association is as expected, but the magnitude of the effect is larger or smaller than expected. Still, the solutions proposed in this article could be used to solve this problem.
The examples also show that unexpected findings in prediction research are not only theoretically challenging but are a phenomenon that can occur in any field of prediction research. When confronted with an unexpected finding, one should evaluate the different reasons for an unexpected finding (i.e., chance, misclassification, selection bias, mixing of effects, heterogeneity effects, intervention effects or a combination of these). Directed acyclic graphs as shown in Figure 1 may help to identify possible causes. As mentioned, heterogeneity or an intervention effect rarely result in unexpected findings, but the clinical examples illustrate that it can occasionally happen. When an unexpected finding is observed, it is more likely that it results from chance, misclassification, selection bias or mixing of effects.
The potential for unexpected findings may differ between study designs. For example, incorrectly conducted case–control studies may be more prone to selection bias than cohort studies. Furthermore, mixing of effects becomes more likely when using retrospective, routinely collected health care registry data, in which the number and detail of observed patient characteristics are typically limited.
In multivariable prediction models, the problem of unexpected findings is likely to be smaller than in the univariable examples shown in this paper, because mixing of effects and intervention effects are accounted for by adding the appropriate covariates to the model.
In conclusion, unexpected findings of the predictor–outcome relation can occur in any kind of prediction research, and likely hamper generalizability and potential uptake of the model for clinical use. Researchers are encouraged to give explanations for possible unexpected findings in their prediction model, including the causes as well as the attempts undertaken to solve the problem, using the proposed framework for causes and solutions for unexpected findings in prediction research.
Key pointsUnexpected predictor–outcome associations may suggest that the prediction model is invalid and has poor generalizability.
Possible causes for unexpected findings in prediction research include chance, misclassification, selection bias, mixing of effects (confounding), intervention effects and heterogeneity.
The type of design or analytical method used to address an unexpected finding depends on the cause of the unexpected finding.
Researchers should report unexpected findings in prediction models, including the potential causes of the unexpected findings and the attempts undertaken to solve them, to improve the potential uptake and impact of the model.
Footnotes
Competing interests: Karel G.M. Moons’ institution has received funds from GlaxoSmithKline, Bayer and Boehringer Ingelheim. No other competing interests declared.
This article has been peer reviewed.
Contributors: Ewoud Schuit, Rolf H.H. Groenwold, Frank E. Harrell Jr., Richard D. Riley and Karel G.M. Moons conceived and designed the study. Ewoud Schuit analyzed the data. Wim L.A.M. de Kort, Anneke Kwee, Ben Willem J. Mol and Karel G.M. Moons contributed data of the clinical examples. Ewoud Schuit and Rolf H.H. Groenwold drafted the manuscript, which all of the authors revised. All of the authors approved the final version submitted for publication.
Funding: Karel G.M. Moons is funded by the Netherlands Organization for Scientific Research (grant 918.10.615 and 9120.8004). Richard D. Riley is supported by funding from the MRC Midlands Hub for Trials Methodology Research at the University of Birmingham (Medical Research Council Grant ID G0800808). The funders had no role in the study design, data collection and analysis, decision to publish or preparation of the manuscript.