Missing the point (estimate)? Confidence intervals for the number needed to treat

The number needed to treat, that is, the average number of patients a clinician needs to treat with a particular therapy to prevent one bad outcome,1 is a translation into clinical terms of the absolute risk reduction derived from a trial. Most clinicians are aware that very small absolute risk reductions translate into large numbers needed to treat, which often helps them to distinguish statistically significant from clinically significant results. For example, in a letter in this issue (page 1652),2 David Gladstone and colleagues use point estimates of the number needed to treat to demonstrate the benefit of tissue plasminogen activator (tPA) in the treatment of stroke. A point estimate represents the single most plausible value in light of the observed data. However the data will generally be consistent with a whole range of values. Along with a point estimate, it is informative to provide a confidence interval reflecting the range of plausible values — and ruling out values outside this range. But the interpretation of confidence intervals for the number needed to treat has some subtleties, and incorrect confidence intervals for the number needed to treat have often been reported.3

The number needed to treat is computed as the reciprocal of the absolute risk reduction. For example, Gladstone and colleagues presented the absolute risk reduction for patients with moderate baseline stroke severity (National Institutes of Health Stroke Scale [NIHSS] between 6 and 10) as being 16.6%. The number needed to treat is thus 1/0.166 or approximately 6. This benefit was statistically significant: the 95% confidence interval for the absolute risk reduction was 0.9%–32.2%. A 95% confidence interval for the number needed to treat is 1/0.009 to 1/0.322 or approximately 3.1–111.1 (Note that taking the reciprocal reverses the order of the limits of the confidence interval.)

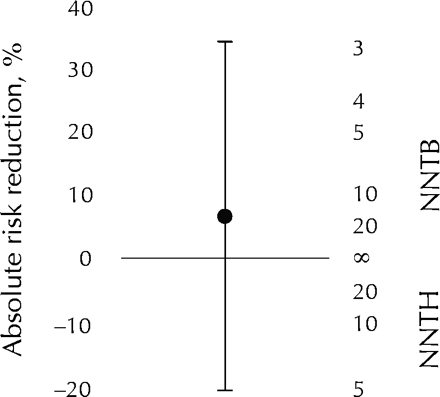
This all seems quite straightforward, that is, until we try the calculation for a nonsignificant result, for example, for patients with low baseline stroke severity (NIHSS score between 0 and 5). The absolute risk reduction was 6.6% with a 95% confidence interval of –20.9% to 34.1%. Naively taking reciprocals gives a number needed to treat of about 15.2 and an apparent 95% confidence interval of –4.8 to 2.9, which does not seem to include 15.2! Clearly something's afoot.

To understand the source of the confusion, note first that the lower limit of the confidence interval for the absolute risk reduction is negative, because the data do not rule out the possibility that tPA is actually harmful for this group of patients. The reciprocal of this lower limit is –4.8, or a “number needed to harm” of 4.8. Altman has suggested that a better description of positive and negative values of the number needed to treat would be the “number needed to treat for one additional patient to benefit (or be harmed),” or NNTB and NNTH respectively.3 The 95% confidence interval for the absolute risk reduction thus extends from a NNTH of 4.8 at one extreme to a NNTB of 2.9 at the other.

To understand what such a confidence interval covers, imagine for a moment that the absolute risk reduction had only just been significant, with a confidence interval extending from slightly more than 0% to 34.1%. The confidence interval for the number needed to treat would now extend from 2.9 to something approaching infinity, denoted ∞. This would indicate that, according to the data, for one additional patient to benefit, a clinician would need to treat at least 2.9 patients (the reciprocal of 34.1%), but perhaps an extremely large number of patients. Thus, when a confidence interval for an absolute risk reduction overlaps zero, the corresponding confidence interval for the number needed to treat includes ∞. This explains the confusion in the case of the patients with low baseline stroke severity: the 95% confidence interval does, after all, contain the point estimate (Fig. 1). Following Altman's suggestion, the estimated number needed to treat and its confidence interval can be quoted as NNTB = 15.2 (95% confidence interval NNTH 4.8 to ∞ to NNTB 2.9). In other words, for this group of patients, it could be that, on average, treating as few as 3 patients with tPA would result in one additional patient benefiting. On the other hand, it could be that, on average, treating as few as 5 patients with tPA would result in one additional patient being harmed.

• Download figure
• Open in new tab
• Download powerpoint

Fig. 1: Confidence intervals for absolute risk reduction and number needed to treat for benefit (NNTB) or harm (NNTH) for patients with low baseline stroke severity. Data from Gladstone et al. ²

The use of the number needed to treat is not without its drawbacks. Its statistical properties are problematic4^,5 and its appropriate application in meta-analysis requires considerable care.6 Particularly with small samples, the commonly used formula for the confidence interval of the absolute risk reduction can give poor results,7 which can have an enormous impact when transformed to the number-needed-to-treat scale. Recently, the use of more refined confidence intervals for the absolute risk reduction has been recommended for obtaining confidence intervals for the number needed to treat.8

It is important to remember that a nonsignificant number needed to treat will have a confidence interval with 2 parts, one allowing for the possibility that the treatment is actually harmful, and the other for the possibility that the treatment is beneficial. Published confidence intervals for the number needed to treat have sometimes included only one of these parts.

CMAJ recommends that when authors express results in terms of the number needed to treat, point estimates for nonsignificant numbers needed to treat should be accompanied by confidence intervals using Altman's notation,3 as described in this commentary.